Power Analysis
Much of what we do with statistics is test the null hypothesis that a treatment has no effect. We choose a small value for the significance criterion, alpha (say, 0.05), to limit rejecting the null hypothesis when it in fact true (Type I error). Power analysis is concerned with Type II errors: accepting the null hypothesis when it is in fact false. When designing experiments, it’s important that there be sufficient power to detect meaningful effects when they exist.
The power of a test of a null hypothesis is the probability that it will lead to the rejection of the null hypothesis. Power is influenced by three parameters:
Alpha: the statistical significance criterion used in the test.
Effect size: the magnitude of the effect of interest.
Sample size.
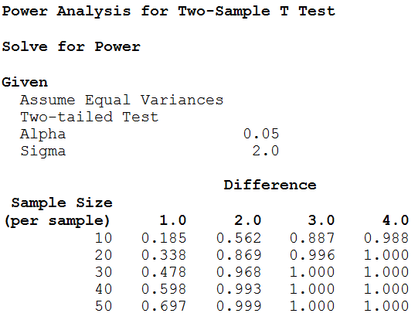
To compute power, you’ll supply values for alpha, effect size, and sample size. When performing power analysis, we often want to determine the sample size required to obtain a powerful test. You can use Statistix to solve for sample size given target values for power and effect size. Many of the power analysis procedures will also solve for effect size given values for power and sample size.
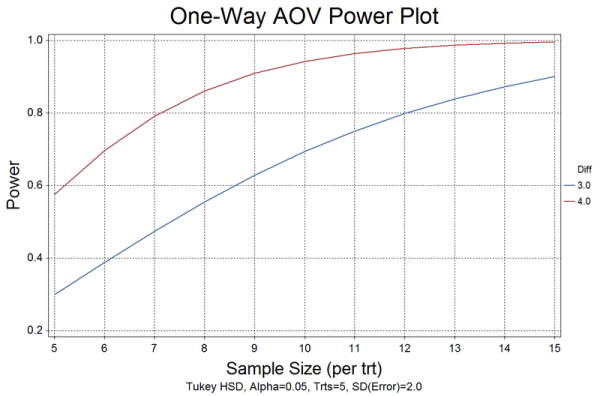
All of the power analysis procedures allow you to produce reports, tables, and plots. A Report is used to compute a single value for power, sample size, or effect size. Select Table to produce a table of computed values (power, sample size, or effect size) for equally-spaced values of one or two input parameters. Select Plot to produce X-Y line plots of power, effect size, or sample size.
Statistix can perform power analysis for a number of balanced analysis of variance designs. It offers two approaches: power of the F test and power of multiple comparisons.
The power analysis procedures available in Statistix are listed below.
One-Sample T Test
Paired T Test
Two-Sample T Test
One-Way AOV
Randomized Complete Block Design
Latin Square Design
Factorial Design
Factorial in Blocks
Split-Plot Design
Strip-Plot Design
Split-Split-Plot Design
Repeated Measures Design
One Proportion
Two Proportions
One Correlation
Two Correlations
Linear Regression
Logistic Regression